One Approach to Computer Generated Music

Robot playing piano

Table of Contents

Introduction

Music is an expression of emotion, shared with its listeners through skilled usage of instruments, both internal and external to the body. Music can also be defined as a sequence of frequencies through time. Computers tend to prefer this second definition.

Algorithmic composition is the usage of algorithms to generate music. Consider the following algorithm:

  1. Sample \(n\) integers from a discrete uniform distribution on the interval \([0, 11]\)
  2. Map each integer to each frequency in the twelve-tone equal temperament scale with a base of Middle C, so \(0\) maps to \(261.6265\ Hz\), \(1\) maps to \(277.1826\ Hz\), etc.
  3. Generate a sound file which consists of the \(n\) frequencies played consecutively for \(0.5\) seconds each
This algorithm is non-deterministic, so can be repeatedly executed to produce novel music! Nonetheless, this algorithm sucks, because its output will tend to sound terrible to humans. Fortunately, music theory offers great tools for describing a structure that sounds good to humans. So, we should be able to greatly improve the algorithm by incorporating some music theoretic ideas.

The paper underlying this blog post defines the following architecture for musical composition:

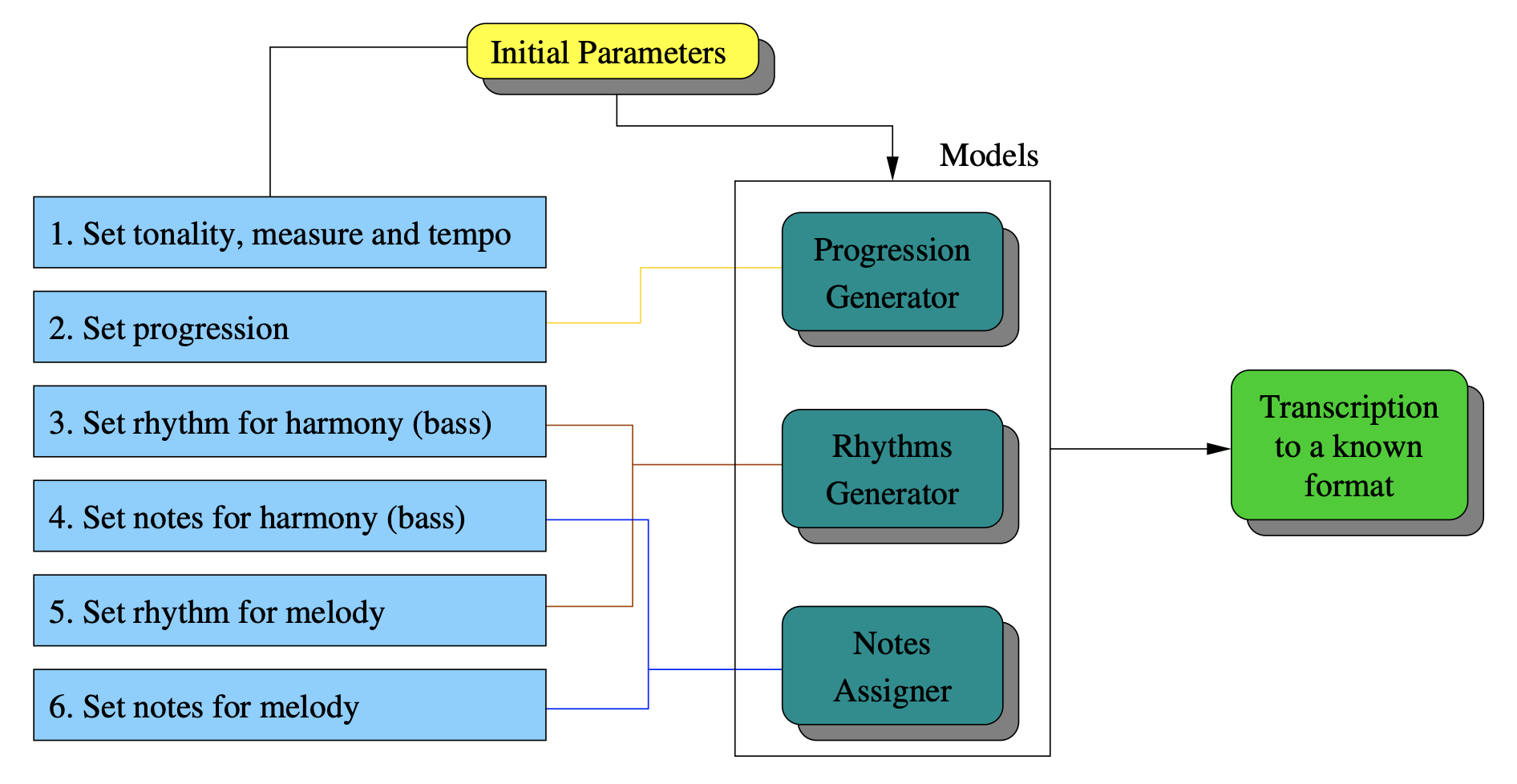
Composition sequence and related models

Each model nicely maps to a computable task. Thus, the collective computable tasks form an algorithm for composition. Although all three models are vital for the production of a pleasing piece, I find the Progression Generator to be by far the most interesting. Consequently, I will dive deep into the Progression Generator, and provide brief commentary and analysis on the Rhythms Generator and Notes Assigner.

Musical Terminology

Let us begin by defining and discussing some musical terms:

  • A tone is a steady periodic sound, and is characterized by its duration, pitch (or frequency), intensity (or loudness), and timbre (or quality)
  • A phrase is a sequence of related tones
  • A chord is a set of multiple tones sounding simultaneously
  • A chord progression is a sequence of chords
  • A scale is a sequence of successive tones within a one-octave range
  • An octave is the interval between one musical tone and another with double its frequency
  • Tonality is the arrangement of tones and/or chords in a hierarchy of perceived relations
    • The perceived relations can be best understood with tones and with respect to a specific scale
    • For example, the C major scale consists of C, D, E, F, G, A, B, a subset of seven of the twelve-equal temperament tones:

      C major scale represented with music notation and degree names


      (The seven notes are played in ascending order with respect to frequency, the C one octave higher than the base C is played, then the notes are played in descending order)

    • Seven tones per octave make up every scale. The first tone in every scale is called the tonic, the second the supertonic, etc. These names describe the perceived relations between the tones. Numbering these tones relative to the tonic makes them degrees. Note that this numbering also applies to chords:

      C major chord progression represented with music notation and degree names


      The chord progression can be denoted by I-IV-V-I

  • Modulation is the process of changing from one tonality to another (i.e. moving tonics from C to G)
  • An anacrusis is a note or sequence of notes which preceeds the first beat of a musical phrase
  • A beat is a punctuating sound
  • Tempo is a pace, denoted in beats per minute
  • A bar or measure is a segment of time corresponding to a specific number of beats played at a specific tempo
  • Time signature specifies the number of beats in a bar

Context-Free Grammars and Probabilistic Context-Free Grammars

The Progression Generator generates a chord progression. “The cornerstone of harmony is the progression underneath the musical content, this is the main structure and foundation of the song. It can be represented by a string of sequential chords over time. Each chord is a degree used in the tonality of the musical phrase”. The authors define an intriguing generative model for chord progressions: a stochastic context-free grammar, also known as a probabilistic context-free grammar (PCFG).

Loosely, a context-free grammar (CFG) is a set of rules and symbols that defines a language. Formally, a CFG is a \(4\)-tuple \(G = (V, \Sigma, R, S)\), where:

  1. \(V\) is a finite set; each element \(v \in V\) is a non-terminal character or variable
  2. \(\Sigma\) is a finite set of terminals, disjoint from \(V\), and is the alphabet of the language defined by the grammar \(G\)
  3. \(R\) is a finite relation in \( V \times (V \cup \Sigma )^{*}\), where the asterisk represents the Kleene star operation. The members of \(R\) are the production rules of the grammar
  4. \(S\) is the start variable used to represent the whole sentence. \(S \in V\)
Production rules can be denoted by:
\(A \rightarrow E\)
where \(A \in V,\;E \in V \cup \Sigma\)

Loosely, a PCFG is a CFG with probabilities attached to each rule. Formally, a PCFG is a \(5\)-tuple \(G = (V, \Sigma, R, S, P)\), where:

  1. \(V, \Sigma, R\) and \(S\) are defined above
  2. \(P\) is a function mapping the set \(R\) to the set \([0, 1]\), such that:
    \(\sum\limits_{E \in X}{P(A \rightarrow E) = 1}\)
    \(\forall A \in V\), where \(X = V \cup \Sigma\)
Production rules can be denoted by:
\(A \rightarrow E\qquad\qquad[p_i]\)
where \(A \in V,\;E \in V \cup \Sigma,\;p_i = P(A \rightarrow E)\)

The paper provides a nice example of a PCFG:

  • \(V = \{S, C\}\)
  • \(\Sigma = \{\)heads, tails\(\}\)
  • \(R, P = \{\)
    • \(\qquad\qquad S \rightarrow C C\qquad\qquad\quad\,[1.0],\)
    • \(\qquad\qquad C \rightarrow\) heads\(\qquad\qquad\;[0.5],\)
    • \(\qquad\qquad C \rightarrow\) tails \(\qquad\qquad\;\;\;[0.5],\)
      • \(\qquad\;\;\}\)
Note that by generating a string with this PCFG, one simulates two fair coin tosses!

The Progression Generator

And now, we are ready to see the PCFG for generating chord progressions:

  • \(\Sigma = \{i, ii, iii, iv, v, vi, viidis, v7\}\), where each of the first seven elements \((i,\,., viidis)\) map to each degree (tonic, supertonic, mediant, subdominant, dominant, submediant, subtonic), and \((v7)\) maps to the dominant seventh chord
  • Production rules and probabilities with annotations:

    Start:
    • \(S' \rightarrow A\;S\;F\qquad\qquad\quad\,[0.3]\qquad\) # Suggestion
    • \(\quad\,\rightarrow S\;F\qquad\qquad\qquad\,[0.7]\)
  • Anacrusis:
    • \(A \rightarrow ana \;v\qquad\qquad\quad\;\,[0.7]\qquad\) # Anacrusis
    • \(\quad\,\rightarrow ana \;i\qquad\qquad\quad\;\,[0.3]\)
  • Phrases:
    • \(S \rightarrow T\;S_1\;D\;T\;S\qquad\;\;[0.35]\qquad\) # Basic Phrases
    • \(\quad\,\rightarrow T\;D\;T\;S\qquad\quad\;\;[0.25]\qquad\) #

    • \(\quad\,\rightarrow T\;M\;D\;T\;S\qquad\;[0.07]\qquad\) # Arpeggios
    • \(\quad\,\rightarrow T\;S_1\;S_2\;T\;S\qquad\;[0.07]\qquad\) #

    • \(\quad\,\rightarrow S_1\;T\;D\;T\;S\qquad\:\,[0.07]\qquad\) # No Tonic Start
    • \(\quad\,\rightarrow D\;T\;S_1\;T\;S\qquad\:\,[0.07]\qquad\) #

    • \(\quad\,\rightarrow T\;S_1\;T\;S\qquad\quad\,\,\,[0.02]\qquad\) # Misc
    • \(\quad\,\rightarrow T\;S_1\;D\;S_2\;T\;S\quad\,[0.02]\qquad\) #
    • \(\quad\,\rightarrow T\;M\;S_1\;D\;T\;S\;\;\;\;[0.02]\qquad\) #

    • \(\quad\,\rightarrow MOD\qquad\qquad\;\;\,[0.06]\qquad\) # Modulation
  • Degree functions:
    • \(T \rightarrow i\qquad\qquad\qquad\quad\;\:\,[0.8]\qquad\) # Tonic
    • \(\quad\,\rightarrow iii\qquad\qquad\qquad\;\;\;[0.1]\qquad\) #
    • \(\quad\,\rightarrow vi\qquad\qquad\qquad\quad[0.1]\qquad\) #

    • \(S_1 \rightarrow iv\qquad\qquad\qquad\;\:\:\,[0.7]\qquad\) # Subdominant
    • \(\quad\,\rightarrow ii\qquad\qquad\qquad\;\;\;\;[0.2]\qquad\) #
    • \(\quad\,\rightarrow vi\qquad\qquad\qquad\;\;\;\,[0.1]\qquad\) #

    • \(D \rightarrow v\qquad\qquad\qquad\quad\:\,[0.4]\qquad\) # Dominant
    • \(\quad\,\rightarrow v7\qquad\qquad\qquad\;\;\;[0.3]\qquad\) #
    • \(\quad\,\rightarrow viidis\qquad\qquad\quad\;[0.2]\qquad\) #
    • \(\quad\,\rightarrow iii\qquad\qquad\qquad\;\;\:[0.1]\qquad\) #

    • \(M \rightarrow iii\qquad\qquad\qquad\;\,\,[1.0]\qquad\) # Mediant

    • \(S_2 \rightarrow vi\qquad\qquad\qquad\;\;\;[1.0]\qquad\) # Submediant
    • End:
    • \(F \rightarrow T\;D\;T\qquad\qquad\quad\;\,[0.7]\qquad\) # End Suggestion
    • \(\quad\,\rightarrow T\;S_1\;T\qquad\qquad\quad\,[0.3]\)

Take a moment to marvel in its glory.

Some things to note:

  • This is not the full grammar. The full grammar is too long to fit in the paper; above is actually a subset of the grammar for major tonalities (there is actually a whole other grammar for minor tonalities)
  • The above is not a formal definition of the grammar; the authors did not provide one. I believe the form they provided the grammar in is more readable, and don’t believe that a formal definition would add much value, hence I decided to replicate the provided representation
  • The grammar reflects the harmonic basis of the genre that the authors wished to model (e.g. ending the song in the tonic degree)
  • The authors assigned probabilities to each rule based on a deep study of J.S. Bach pieces

To get a better understanding of the PCFG, let's take a look at a short, high-probability output:

\(S' \rightarrow S\;F\)

\(S \rightarrow T\;S_1\;D\;T\;S\)
\(F \rightarrow T\;D\;T\)
\(= T\;S_1\;D\;T\;S\;T\;D\;T\)

\(T \rightarrow i, \forall T\)
\(S_1 \rightarrow iv\)
\(D \rightarrow v, \forall D\)
\(S \rightarrow \epsilon\)
\(= i\;iv\;v\;i\;i\;v\;i\)

= I-IV-V-I-I-V-I

\(\epsilon\) is notation for empty string. Note that there is no production rule \(S \rightarrow \epsilon\) present in the above grammar; length is handled separately. The production rule serves as a convenient hack to generate the above chord progression.

Here's what the chord progression sounds like:



Here is another nice chord progression, generatable by the PCFG with a relatively high probability, and its audio:

\[i\;iv\;v\;i\;iii\;vii\;vi\;iii\;v\;i\;\]

= I-IV-V-I-III-VII-VI-III-V-I


Although the grammar produces nice chord progressions, there are some notable limitations.

CFGs cannot describe the structure of some languages. For example, CFGs cannot capture languages that exhibit cross-serial dependencies:

Cross-serial dependencies

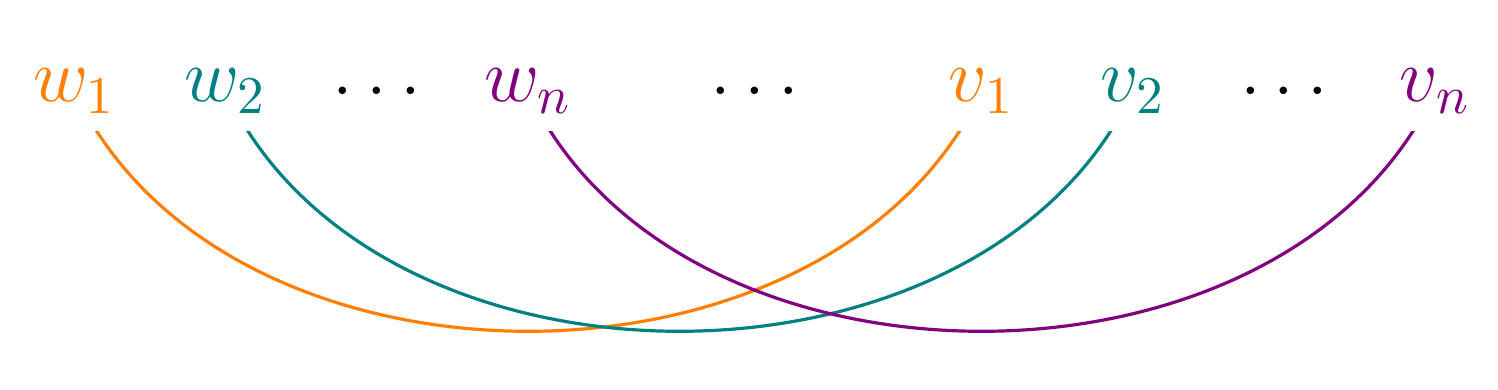
The language of strings of the form: \[a^mb^nc^md^n\] has cross-serial dependencies, hence it is non-context free.

The language: \[a^mb^na^mb^n\] also is not context free. Imagine that \(a\) and \(b\) are chord progressions. This pretty interleaving of chord progressions cannot be described by a CFG, and thus cannot be generated by a PCFG.

The probability of each rule in a PCFG is fixed upon definition. This means that there is no way to augment the probability distribution of rules when certain rules are applied during the generation of a string. It would be nice to be able to do this, since it could allow for biasing of the probability distribution such that repeated structures or patterns have a high chance of occurring throughout the chord progression. This could make for a cool extension of PCFGs: "aware" or "self-modifying" PCFGs.

Instead of defining an "aware" PCFG, it is easier to use already-existing, more powerful structures. Context-sensitive grammars (CSGs) are an extension of CFGs that allow for a mixture of terminal and non-terminal symbols on both the left- and right-hand side of each production rule. Unrestricted grammars are an extension of CSGs that allow for any production rules that have non-empty left-hand sides. Unrestricted grammars counter the two problems described in the previous paragraphs, since they are equivalent to Turing machines, which is to say any computer algorithm. We can certainly define algorithms that generate languages containing cross-serial dependencies, and define algorithms for augmenting the probability of each rule in a PCFG upon rule application.

The Rhythms Generator

The Rhythms Generator generates a rhythm for the piece. It receives as input the tempo and time signature of the piece, and outputs durations for each note and chord.

The authors of the paper define three categories for each measure in a piece:

  • Normal measures: Bars from within the progression with no radical meaning other than advancing the piece
  • Special measures: Pivotal bars or with special meaning
  • Final measures: Final bars of phrases or the whole theme

Loosely, the duration of each note and chord is determined by sampling from the probability distribution for the encapsulating measure's category (normal, special or final). To provide cohesion between measures, a decision tree is sampled from, determining how rhythm should (or should not) change from measure to measure.

The Notes Assigner

The Notes Assigner assigns notes to form the melody. The first note of each measure is selected to match the base of the first chord for that measure. The remaining notes are determined relative to the previous note, according to a probability distribution:

Composition sequence and related models

An interesting observation is that the distribution has bias towards the third and fifth intervals, since these notes make a basic chord with the base (previous) note, avoiding dissonance, making everything sound pleasant. For example, with a current note and chord of C and C major, there is a high chance of the following note being E or G, mirroring the C-E-G notes of the C major chord.

A Piece Generated By The Models

With initial parameters:

  • Tonality: G major
  • BPM: 110
  • Measure: \(\genfrac{}{}{0pt}{}{4}{4}\) (binary)
  • Length: Approx. 25 bars

The following piece was generated:

Composition sequence and related models

The authors provide some analysis of the piece:

"The song's initial tonality is G major modulating to its relative minor (G minor) at measure \(6\) and keeping this tonality until finishing. Harmonically the song is marking the progression I-VI-I and the progression I-III-I with an intersection containing the common progression I-II-V7-I and finally finishing in the tonic degree (G minor).

Melodically the song is overall simple having upward intervals to make a tension or climax at various points (measures \(3, 8, 10, 13, 16, 21\)) and then with downward intervals to relieve the ear of this. It is to note that the climax at bar \(16\) coincides with the chord V7 (this chord has a bit of dissonance).

Rhythmically there were two basic rhythms generated for the bass and the melody line, the reader may see that the trivial rhythm for the base (just one whole note) has a more complex counterpart in the melody each time it is played. The other two rhythms are fairly normal that make way to the following more complex rhythm. Also the global rhythm is far from chaotic."

Final Remarks

I was ecstatic when first discovering the paper underlying this blog post, because after learning that one can create CFGs that describe the main structures of the English language [page 6], I was curious to further explore the expressive power of CFGs. Eventually, I had the idea of applying it to the language of music, which prompted my discovery of the paper.

Nonetheless, I am disappointed by the paper's general lack of rigour and completeness when describing and showcasing each model. Furthermore, the link provided on page 11 to see other generated pieces and play around with a beta version of the assistant is broken.

For me, this paper provides some great preliminary analytical tools and models for describing Bach's compositions, and music theory in general, in terms of computation. It would be cool to push these ideas and models further, perhaps using more sophisticated tools (i.e. probabilistic CSGs and probabilistic unrestricted grammars), and even trying to integrate the disjoint models together, to provide more cohesion among the different components of the generated pieces.

Notes

The Rhythms Generator
  • I am unsure how measures are classified
  • I am unsure how the Rhythms Generator differs for the melody and the chord progression
  • I am unsure why there is a duration of \(1.5\), since I believe it is standard in Western music to only use durations that are a power of two of the length of each bar. A duration of \(1.5\) is possible with dot notation, though this complexity seems beyond the simple model
  • I am unsure how the proposed probabilities fulfill the probability rules. Perhaps the authors truncated the full table for the sake of brevity, explaining why the column's values do not sum to 1?

Sources

Post image: "Robot music" by Possessed Photography, hosted by Unsplash, license

Underlying paper: Salim Perchy, Gerardo Sarria. Musical Composition with Stochastic Context-Free Grammars. 8th Mexican International Conference on Artificial Intelligence (MICAI 2009), Nov 2009, Guanajuato, Mexico. hal-01257155, URL

Introduction
Musical Terminology
Context-Free Grammars and Probabilistic Context-Free Grammars
The Progression Generator
The Rhythms Generator
  • pp. 7-9, Salim Perchy, Gerardo Sarria. Musical Composition with Stochastic Context-Free Grammars. 8th Mexican International Conference on Artificial Intelligence (MICAI 2009), Nov 2009, Guanajuato, Mexico. hal-01257155

The Notes Assigner
  • pp. 9, Salim Perchy, Gerardo Sarria. Musical Composition with Stochastic Context-Free Grammars. 8th Mexican International Conference on Artificial Intelligence (MICAI 2009), Nov 2009, Guanajuato, Mexico. hal-01257155

A Piece Generated By The Models
  • pp. 10-11, Salim Perchy, Gerardo Sarria. Musical Composition with Stochastic Context-Free Grammars. 8th Mexican International Conference on Artificial Intelligence (MICAI 2009), Nov 2009, Guanajuato, Mexico. hal-01257155
  • Sugerencia audio

Final Remarks
Notes