One Approach To Computer Generated Music

Robot playing piano

Table of Contents

Introduction

Music is an expression of emotion, shared with its listeners through skilled usage of instruments. Music can also be defined as a sequence of sounds over time. Computers tend to prefer this more simplistic second definition.

For example, it is easy to tell a computer to randomly select some number of notes from a piano's C, D, E, F, G, A, B, and play each selected note for half a second.

While this process could generate the melodies of famous pieces, it is very unlikely to. Besides, good songs often involve more components, such as rhythm and chord progressions. (I'll provide some examples for this and other relevant musical terms).

The paper which inspired this blog post provides the following template for a computer to generate good music with:

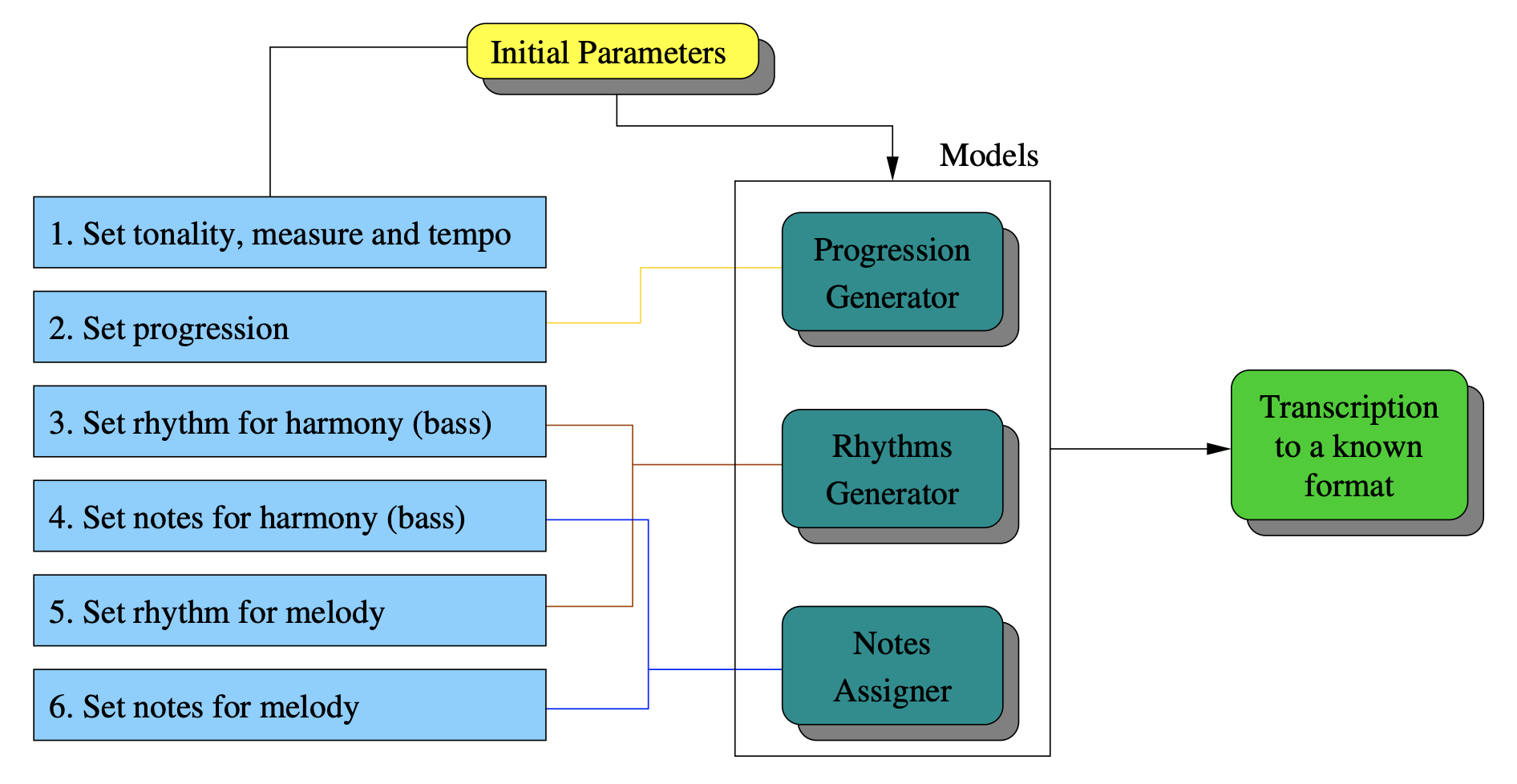
Composition sequence and related models

Don't worry about the specifics. It basically says that by specifying a few musical elements of a song, such as the key, tempo and length, and inputing them into a computer, you can generate a nice song with the inputted key, tempo and length.

Note that the middle layer consists of three models. Each model is a sub-component of the overall process that generates some element of the output song. For example, the Progression Generator generates the song's chord progressions.

The purpose of this blog post is to briefly explain how each model works, with a heavier focus on the Progression Generator, simply because I think it is the coolest.

Musical Terms

But first, some musical terms.

All melodies and chords consist of notes (for example, C on a piano). A melody is a sequences of notes played over time. For example:



A chord is multiple notes playing at the same time. A chord progression is a sequence of chords played over time. For example:


This chord progression consists of four chords.

The chords sound good together because they contain notes from the same key. A key is a group of notes. In this case, the chords are from the key C major, which is the name for the group of notes C, D, E, F, G, A, B. Here is what these notes sound like:


The audio is of the C major scale, which is the playing of the notes C, D, E, F, G, A, B, C, B, A, G, F, E, D, C.

The ordering of the notes in each key is deliberate. In the C major key, the first note, C, has the lowest pitch. Meanwhile the seventh note, B, has the highest pitch.

In the same way that notes have names, chords have names too. The chord consisting of the notes C, E, G is the first chord in the C major key (since the chord's lowest pitch note is the note with the lowest pitch in the key), so it is referred to as I (1). Thus, chord progression you listened to above can be described by I-IV-V-I.

While notes are the base block for melodies and chords, beats are the base block for rhythm. For example, the tempo of a song is the speed of the song, and is measured in beats per minute.

The Progression Generator

The Progression Generator generates a chord progression. In the Introduction, I said that we could easily generate a melody by telling a computer to randomly select some number of notes from a piano's C, D, E, F, G, A, B. So surely we can easily generate a chord progression by telling a computer to randomly select some number of chords from a piano's I, II, III, IV, V, VI, VII?

While this is true, in the same way that random combinations of notes often sound bad together, random combinations of chords also often sound bad together too.

Fortunately, music theory tells us what chord progressions sound good together. So, we want to somehow restrict the computer's choices to combinations of chords that sound better than say I-I-I-I.

Enter, context-free grammars and probabilistic context-free grammars.

Loosely, a context-free grammar (CFG) is a set of rules and symbols that defines a language. So for example, in English, every word belongs to some category — every word is either a noun, verb, adjective, etc. We can define the relationship between adjectives and nouns with the following rule:

\(Noun \rightarrow Adjective\;Noun\)

This essentially means, whenever you have a noun, you can replace it with an adjective and then that noun. For example, if I start with the noun 'Omer', I can replace it with 'clever Omer'. I can repeat this again, since my phrase still contains a noun, and generate 'clever sexy Omer'. I could keep going. Shall I? stop it ;)

A probabilistic context-free grammar (PCFG) is just a CFG with probabilities attached to the rules. So for example, I could describe the tossing of a coin with a PCFG with these rules:

\[Coin \rightarrow heads\quad[50\%]\] \[ Coin \rightarrow tails\quad\;\:[50\%]\]

This means that every symbol Coin has a 50% chance of becoming heads or tails. So, to toss two coins, I can feed the PCFG the phrase 'Coin Coin', and let the rules and their probabilities generate the outcome.

Now we are ready to make sense of the Progression Generator proposed in the paper that inspired this blog post. It is defined by a PCFG, whose rules and probabilities represent common chord progressions. As you can imagine, it is quite complicated, and consists of many rules and symbols. If this isn't so clear, imagine how many rules and symbols we would have to add to our above CFG to encapsulate all of the grammatical rules in the English language.

Let's take a look at a short, high-probability output from the PCFG:

1) We start with the starting symbol \(S'\).

2) We replace \(S'\) with the symbols \(S\;F\) by applying one of the rules of the PCFG. \(S\) is supposed to represent a general chord progression, and \(F\) is supposed to represent a finishing chord progression.

3) We replace the \(S\) in \(S\;F\) with the sequence \(T\;S_1\;D\;T\;S\), and we replace the \(F\) with \(T\;D\;T\). Notice that in the same way that our earlier rule

\[ Noun \rightarrow Adjective\;Noun\]

includes Noun on both sides, the rule we applied here includes S on both sides. This just means that we can keep applying the same rule. Earlier, I repeatedly applied the rule to flatter myself — here, we can repeatedly apply the rule to generate as many sequences of chords as we would like.

4) We have the phrase \(T\;S_1\;D\;T\;S\;T\;D\;T\). Let's apply rules to replace every \(T\) with an I, \(S_1\) with IV, every \(D\) with a V, and let's just drop the \(S\). Finally, we have applied enough rules to the abstract symbols to recover a sequence of chords! We have ended up with I-IV-V-I-I-V-I.

Here's what the chord progression sounds like:



I generated another chord progression, I-IV-V-I-III-VII-VI-III-V-I, by applying different rules to the symbols. Here's how this one sounds:



The longer sequence does a better job of showcasing the range of musical ideas embedded in the PCFG. If you have some knowledge of music theory, I encourage you to take a look at the rules given in the paper [pages 6 and 7], and see if you can recognize any common chord progressions.

Although the PCFG successfully produces pleasant chord progressions, there are considerable limitations.

For example, cross-serial dependencies cannot be captured by the rules of any PCFG:

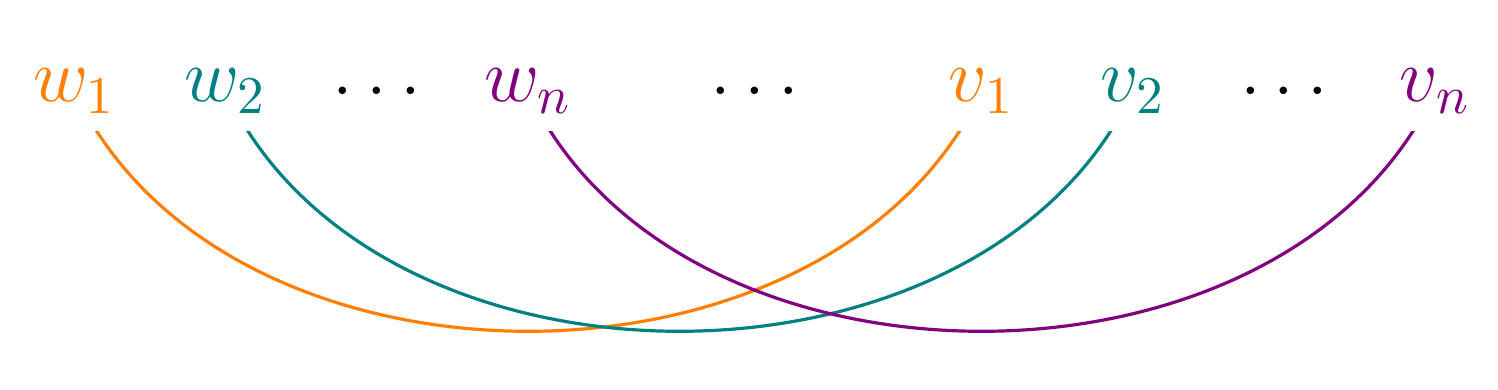
Cross-serial dependencies

Imagine that \(w_1\) and \(v_1\) are the same chord progression, and that \(w_2\) and \(v_2\) are also the same chord progression. This pretty interleaving of chord progressions, which represents a valid and probably enjoyable musical idea, is impossible to produce with a PCFG.

The Rhythms Generator

The Rhythms Generator generates a rhythm for the piece by assigning durations to each note and chord.

The authors of the paper define three categories for each measure (small segment of a song) in a piece:

  • Normal measures: Segments of the song with no radical meaning
  • Special measures: Pivotal segments with special meaning
  • Final measures: Final sections of a musical idea, or the entire piece

The duration of each note and chord is determined by the category of the measure it belongs to. Each category has different probabilities of containing short and long duration notes and chords.

One helpful observation is that the final measures have a high chance of containing notes and chords with a longer duration, presumably to add significance.

The Notes Assigner

The Notes Assigner assigns notes to form the melody.

The first note of each small segment of the song is selected to match the base of the first chord for that section. For example, if a segment begins with the chord C-E-G, the first note in that segment's melody will be a C.

The remaining notes are determined with probability in such a way that there is a high-likelihood of generating a pleasant sounding melody. The trick is to assign probabilities to the next note relative to the current note, since we understand these relative relationships well.

For example, with a current chord and note of C-E-G and C, we assign a high chance of the next note being E or G, to mirror the C-E-G notes of the current chord.

A Piece Generated By The Models

The following piece, with a key of G major, a tempo of 110 beats per minute, and a length of approximately 25 bars, was generated by all three models:

Composition sequence and related models

The authors provide some analysis of the piece:

"The song's initial tonality [key] is G major modulating to its relative minor (G minor) at measure \(6\) [last section on the first line of the sheet music] and keeping this tonality until finishing. Harmonically the song is marking the progression I-VI-I and the progression I-III-I with an intersection containing the common progression I-II-V7-I and finally finishing in the tonic degree (G minor) [the base chord].

Melodically the song is overall simple having upward intervals to make a tension or climax at various points (measures \(3, 8, 10, 13, 16, 21\)) and then with downward intervals to relieve the ear of this. It is to note that the climax at bar 16 coincides with the chord V7 (this chord has a bit of dissonance [harshness]).

Rhythmically there were two basic rhythms generated for the bass and the melody line, the reader may see that the trivial rhythm for the base (just one whole note) has a more complex counterpart in the melody each time it is played. The other two rhythms are fairly normal that make way to the following more complex rhythm. Also the global rhythm is far from chaotic."

Final Remarks

I was ecstatic when first discovering the paper underlying this blog post, because after learning that one can create CFGs that describe the main structures of the English language [page 6], I was curious to further explore the expressive power of CFGs. Eventually, I had the idea of applying it to the language of music, which prompted my discovery of the paper.

The paper does a great job of providing preliminary analytical tools and models for describing Bach's compositions, and music theory in general, in terms of a framework that computers understand.

Nonetheless, I am disappointed by the paper's general lack of rigour and completeness when describing and showcasing each model. Detail is missing to recreate everything oneself. The link provided on page 11 to see other generated pieces and play around with a beta version of the assistant is broken.

It would be cool to push the embedded ideas and models further, perhaps using more sophisticated tools (i.e. probabilistic CSGs and probabilistic unrestricted grammars), and even trying to integrate the disjoint models together, to provide more cohesion among the different components of the generated pieces.

Sources

Post image: "Robot music" by Possessed Photography, hosted by Unsplash, license

Underlying paper: Salim Perchy, Gerardo Sarria. Musical Composition with Stochastic Context-Free Grammars. 8th Mexican International Conference on Artificial Intelligence (MICAI 2009), Nov 2009, Guanajuato, Mexico. hal-01257155, URL

Introduction
  • Chord progression
  • Fig. 3., Salim Perchy, Gerardo Sarria. Musical Composition with Stochastic Context-Free Grammars. 8th Mexican International Conference on Artificial Intelligence (MICAI 2009), Nov 2009, Guanajuato, Mexico. hal-01257155
  • Key
  • Tempo

Musical Terms
The Progression Generator
The Rhythms Generator
  • Measure
  • pp. 7-9, Salim Perchy, Gerardo Sarria. Musical Composition with Stochastic Context-Free Grammars. 8th Mexican International Conference on Artificial Intelligence (MICAI 009), Nov 2009, Guanajuato, Mexico. ffhal-01257155

The Notes Assigner
  • pp. 9, Salim Perchy, Gerardo Sarria. Musical Composition with Stochastic Context-Free Grammars. 8th Mexican International Conference on Artificial Intelligence (MICAI 009), Nov 2009, Guanajuato, Mexico. ffhal-01257155

A Piece Generated By The Models
  • pp. 10-11, Salim Perchy, Gerardo Sarria. Musical Composition with Stochastic Context-Free Grammars. 8th Mexican International Conference on Artificial Intelligence (MICAI 2009), Nov 2009, Guanajuato, Mexico. hal-01257155
  • Sugerencia audio
  • Tonality
  • Degree
  • Dissonance

Final Remarks